Zrcadlení

Dobře známý jev zrcadlení je na Obr. 7 znázorněn v pojetí QED. Obrázek Obr. 7 představuje zjednodušenou ilustraci Pravidla č. 3, podle něhož foton se ze zdroje světla může dostat k detektoru různými cestami, aby tam vytvořily obraz zdroje. Všechny možné trasy fotonu (svazku fotonů) jsou zde reprezentovány přímkovými paprsky v souladu s Pravidlem č. 6.

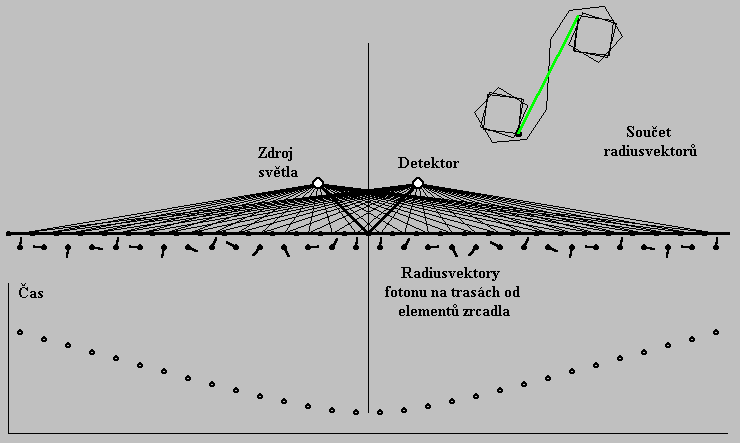
Obr. 7  Zrcadlení podle QED - program zrcadleni.exe

Pod zrcadlem jsou znázorněny radiusvektory fotonu (svazku fotonů) po dopadu na detektor. Všechny mají stejnou délku, ale různou fázi úměrnou délce dráhy od zdroje k detektoru. Díky Pravidlu č. 5 pod každým bodem zrcadla máme jen jeden radiusvektor i v případě svazku fotonů.

V spodní části Obr. 7 je graf znázorňující čas, který foton potřebuje, aby přeletěl od zdroje světla k detektoru. V okolí kolmice v bodě s nejnižším časem jsou radiusvektory přibližně stejně orientovany, a proto nejvíc přispívají k součtovému radiusvektoru. Dále od této kolmici jsou radiusvektory různě orientovány, a proto jejich příspěvky se k celkovému součtu vzájemně ruší.

Tlustou černou čarou je znázorněn paprsek odpovídající nejmenšímu času. Vidíme, že vzhledem k vertikále se úhel dopadu tohoto paprsku na zrcadlo rovná úhlu odrazu. To je dobře známý zákon zrcadlení geometrické optiky, která vychází z Newtonovy představy, že světlo je proud blíže nespecifikovaných částiček zvaných "korpuskule".

Podle Obr. 7 by se dalo usuzovat, že časti zrcadla vzdálené od středu mezi zdrojem světla a detektorem nehrají žádnou roli, protože jejich příspěvky k součtovému radiusvektoru nepřispívají, nebo jen velmi málo, o čem svědčí i "zakroucené" konce sumarizační křivky. V následujícím oddílu - Difrakce na mřížce - ukážeme, jak lze tyto vzdálené části zrcadla přimět k tomu, aby byly hlavním aktérem zrcadlení.