Úplný odraz

Obrázek a interaktivní program v oddílu Lom paprsků světla ilustruje Snellův zákon z pohledu QED - součet radiusvektorů fotonu po všech jeho trasách. Holandský fyzik Willenbrod Snell (1591-1626) odvodil pomocí vlnové teorie světla po něm nazvaný zákon, který říká: při šíření záření pod úhlem dopadu β (od kolmice na rozhraní) z prostředí opticky hustšího do opticky řidšího se paprsky lámou směrem od kolmice pod úhlem α podle vztahu sinα /sinβ = c_α/c_β = n_β/n_α, kde c_α a c_β je rychlost světla v opticky řidším resp. hustším prostředí a n_β, n_α je index lomu opticky hustšího resp. řidšího prostředí.

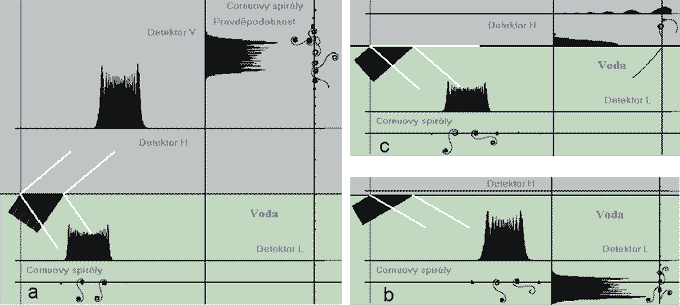
Obr. 17  a)Lom paprsků, b) úplný odraz paprsků, c) lom/odraz paprsků pro mezní úhel dopadu.
- program uplny-odraz.exe

V dalším za opticky řidší prostředí budeme považovat vakuum, pro které je index lomu z definice n_α = 1 a tudíž sinα = n_β × sinβ. Úhel dopadu β, pro který je α = 90°, se nazývá mezní úhel. Pro vodu je n_β = 1.33 a mezní úhel je cca 48°. Pro jistý druh skla je n_β= 1.55 a mezní úhel je cca 42°. Pro úhel dopadu β větší než je mezní nemá rovnice sinα = n_β × sinβ řešení a tudíž Snellův zákon tento případ neřeší. Ve skutečnosti je to situace, kdy se rozhraní chová jako zrcadlo a paprsky se od něho odrážejí jako v zrcadle: úhel dopadu se rovná úhlu odrazu. Je to úkaz, který se využívá např. při konstrukci optických kabelů.

Obr. 17 ilustruje lom paprsků a úplný odraz podle teorie QED. Vlnovou teorií řečeno, na rozhraní dopadá rovinná vlna pod úhlem β. V mluvě QED to znamená, že všechny reprezentativní trasy fotonu v látce jsou vzájemně souběžné. Dopad fotonu registrují tři detektory: vertikální detektor V, horizontální detektor H ve vakuu a horizontální detektor L v látce. Kromě pravděpodobnostních obrazců pro vybrané body na detektorech jsou znázorněny i Cornuovy spirály. Bílé přímky naznačují směr paprsku podle zákonů geometrické optiky.

Fáze radiusvektoru fotonu při dosažení rozhraní závisí na úhlu dopadu β svíraného s kolmicí na rozhraní. V interaktivním programu uplny-odraz.exe se počítá s tím, že od rozhraní se foton šíří všemi trasami k detektorům, přičemž v látce je efektivní rychlost fotonu n_β krát menší než ve vakuu.

Na Obr. 17c je znázorněna situace, kdy mezní úhel β je právě ten kritický. Je-li povolena personifikace, tak v tomto případě foton neví zda má pokračovat ve vakuu nebo v látkovém prostředí. Existuje jistá pravděpodobnost, že foton od rozhraní pokračuje ve vakuu. Ukazuje to pravděpodobnostní obrazec pro vertikální detektor V a také pro horizontální detektor H, když je umístěn dostatečně blízko k rozhraní, aby obrazec nevypadl mimo obrazovku. Existuje však také jistá pravděpodobnost, že foton se odrazí od rozhraní nazpět do látkového prostoru, jak to dokládá pravděpodobnostní obrazec na horizontáním detektoru L.

Na Obr. 17b je zobrazený pravděpodobnostní obrazec na detektoru V pro úplný odraz. Pro neúplný odraz tento obrazec není vidět, jelikož se umístil mimo délku detektoru V. Jeho polohu si lze domyslet, když bílé úsečky prodloužíme až k pomyslné linii vertikálního detektoru V. Bílé úsečky představují paprsky odražené (lomené) podle zákonů geometrické optiky. Měřítka pravděpodobnostních obrazců nejsou v relaci s relativní pravděpodobnosti dopadu fotonu na příslušný detektor. Jinými slovy, grafické konstanty výpočtu byly zvoleny tak, aby se pravděpodobnostní obrazce zobrazily v ilustrativní velikosti.

Všechny pravděpodobnostní obrazce jsou spočítány metodou sumarizace radiusvektorů všech tras od rozhraní k detektorům bez použití Snellova zákona lomu nebo zákona zrcadlení. A právě naopak, tyto obrazce potvrzují správnost uvedených zákonů geometrické optiky.