Holografie
 
animace Feynmanovou metodou dráhových součtů

Počítačová animace holografie přispívá k pochopení způsobů, kterými Příroda vytváří své kouzla, jelikož v simulaci můžeme postup sledovat krok za krokem. V případě světla je univerzálním jevem interference, která se, závisle na okolnostech, může jevit jako difrakce (ohyb), refrakce (lom), reflekce (zrcadlení), disperze atd. Metoda dráhových součtů usnadňuje počítačovou animaci tím, že zde v podstatě vystačíme s elementární matematikou počítání délky dráhy a součtu vektorů. Cílem počítačové animace není znázornit virtuální objekt jak ho vidí pozorovatel přes hologram, ale ilustrovat rekonstruované světelné pole a konfrontovat ho s původním polem rozptýleným přes průzor.

Z pohledu vlnové teorie koherentního světla se světelné pole v každém bodě prostoru vyznačuje amplitudou vlny a její fází. Klasická fotografie zaznamenává jenom amplitudu vlny a informace o fázi se ztrácí. V důsledku toho při prohlížení fotografie pozorovatel vidí obraz plošně bez paralaxu.

Holografie je způsob záznamu úplné informace o světelném poli v místě, kde se nachází fotografická deska. To znamená, že se zde uchovává informace jak o amplitudě, tak také o fázi vlny. Takto vytvořený obraz na fotografické desce se nazývá hologram, kterým lze vnímat obraz objemově s paralaxy. Pouhým pohledem na hologram nelze rozeznat snímaný objekt, protože je to jen interferenční obrazec jemných proužků tak hustých, že pouhým okem nejsou ani k rozeznání.

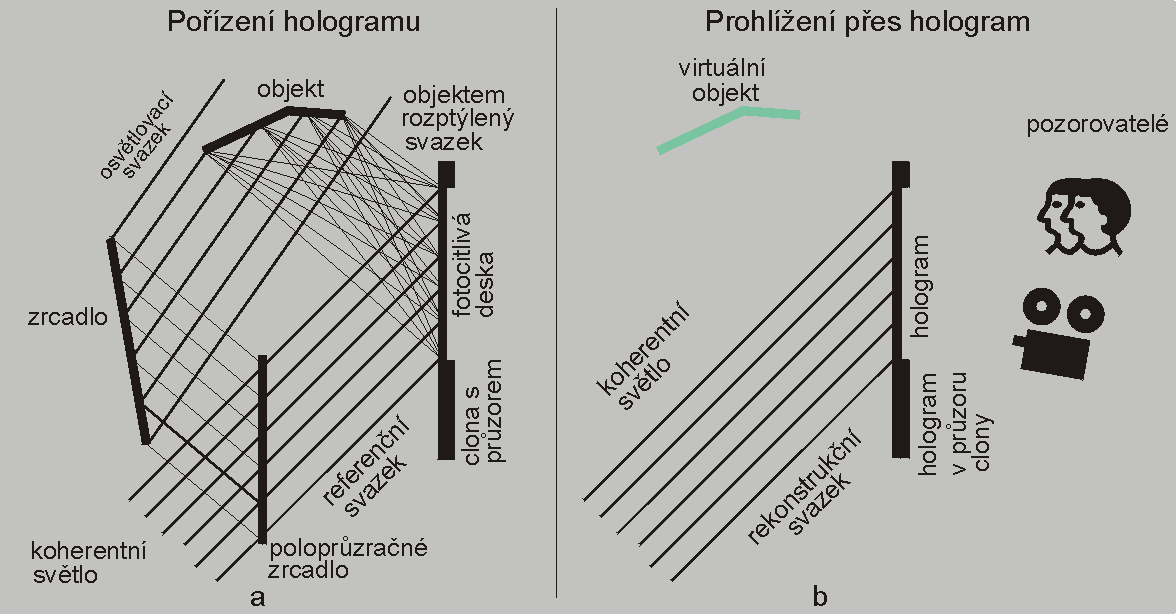
Obr. 19 Holografie v pojetí vlnové teorie světla

Zaznamenání scény hologramem a její prohlížení přes hologram ilustruje Obr. 19. Podstata holografie spočívá v tom, že snímaná scéna (objekt) je ozařována koherentním světlem (osvětlovací svazek) a současně je ozařována týmž koherentním světlem (referenční svazek) i fotocitlivá deska. Odrazené světlo od objektů scény interferuje se světlem referenčního svazku a na fotocitlivé desce vytváří plošný interferenční obrazec. Nejlepším zdrojem koherentního světla je laser. Rozlišovací schopnost fotocitlivého materiálu musí být veliká - cca 5000 linií na jeden milimetr pro viditelné světlo.

Holografický obraz lze vnímat prosvícením hologramu koherentním světlem, čím se za clonou obnoví světelné pole (elektromagnetické pole), co umožní pozorovatelům zaznamenávat tento obraz (virtuální objekt). Pozorovatelem nemusí být jen člověk se svými oči, ale libovolný přístroj schopný zaznamenávat elektromagnetické pole (fotografický přístroj - například).

Na Obr.19 znázorněný způsob pořízení hologramu není jediný, nicméně je vhodný k ilustraci holografie pomocí počítačové animace z pohledu kvantové elektrodynamiky (QED). Podle této teorie jediným „aktérem“ světla je foton se svými neobyčejnými vlastnostmi. Ze zdroje letí jeden jediný foton současně všemi možnými trasami (pokud mu v tom nebrání překážka, např. clona) a v místě dopadu je schopen vytvářet interferenční obrazce, křižují-li se dráhy. V grafické ilustraci jsou všechny trasy znázorněny jen tzv. reprezentativními dráhami jako přímky - viz Rozptýlené trasy fotonu. V grafické interpretaci foton znázorňujeme vektorem (kvantovým vektorem), který po své reprezentativní dráze rotuje rychlostí úměrnou kmitočtu koherentního světla - viz detail-interference.exe.

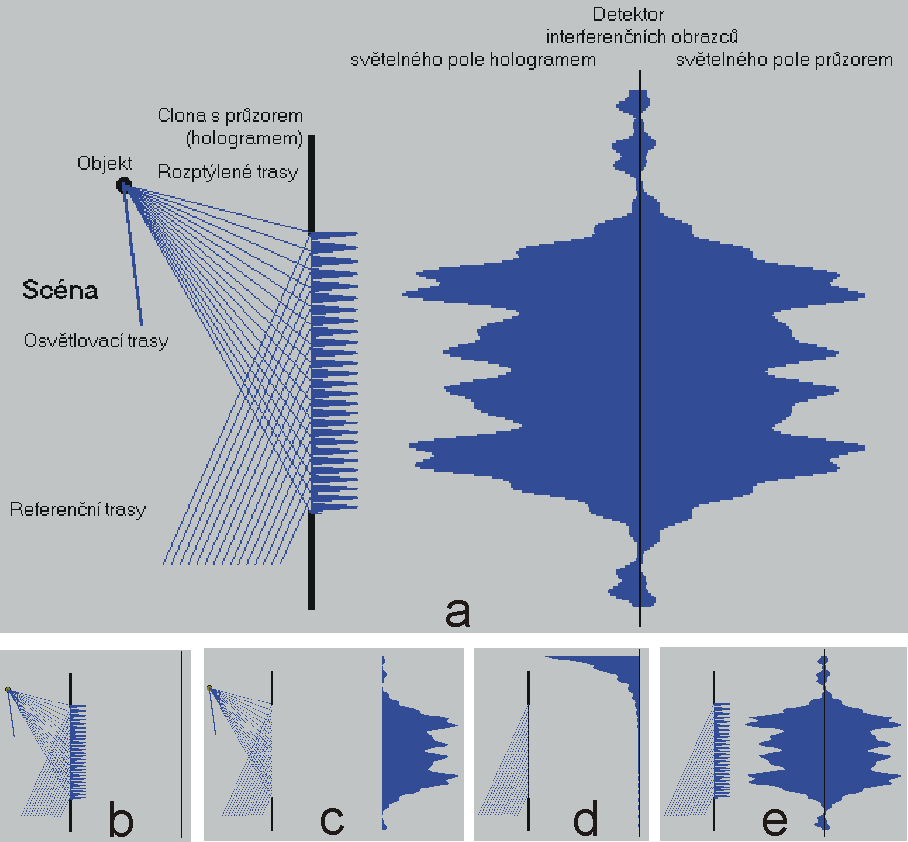
Po tomto krátkém ohlédnutí se o podstatě neobyčejné teorii světla výklad počítačové animace budeme sledovat podle Obr. 20. Jak jsme již uvedli, cílem není znázornit obraz objektu jako ho vidí pozorovatelé, ale ilustrovat rekonstruované světelné pole a konfrontovat ho s původním polem rozptýleným přes průzor. Pole ilustrujeme interferenčními obrazci (pravděpodobnost dopadu fotonu) v místě detektoru nebo fotocitlivé desky, jejichž hodnota v daném bodě je úměrná kvadrátu délce vektorového součtu vektorů, které sem rotovaly všemi trasami. Animací tak na liniovém detektoru porovnáváme původní světelné pole přes průzor a rekonstruované přes hologram.

Zobrazovaným objektem scény je malá kulička - jediný bod prostoru. Proto k ní vystačíme jen s jednou osvětlovací trasou. Od bodového objektu foton pokračuje všemi trasami k průzoru. Foton sem dorazí také referenčními trasami. V průzoru tak je foton schopen vytvořit interferenční obrazec (Obr. 20b). Je-li do průzoru vložená fotografická deska, a necháme-li ji bombardovat množstvem fotonů, pak lokálně zšedne v rozsahu bílá-černá úměrně velikosti interferenčního obrazce v daném místě. Tak vznikne hologram. V dalším výkladu počítačové animace slovem hologram budeme označovat interferenční obrazec v průzoru.

Ke každému bodu detektoru letí foton trasami od všech bodů průzoru. Tyto vějíře tras na obrázku nejsou uvedeny. Druhý spodní obrázek (Obr. 20c) ukazuje interferenční obrazec průzoru (bez hologramu) od rozptýleného a referenčního svazku světla. Toto je přestavitel původního světelného pole, se kterým se porovnává obrazec rekonstruovaného pole.

Obr. 20  Počítačová animace holografie - program holografie.exe

Na třetím spodním obrázku (Obr. 20d) vidíme interferenční obrazec fotonu letícího referenčními trasami přes průzor k detektoru. Je to interferenční obrazec difrakce na štěrbině, jak jsme se s ním setkali již v oddílu Interference a difrakce na štěrbině. Obrazec svou „krajkou“ dosahuje až na detektor, přestože osvětlená oblast podle pravidel geometrické optiky je vysoko nad ním.

Vložíme-li do průzoru hologram (Obr, 20e), pak délka vektoru je modulována hologramem. Znamená to, že délka vektoru před průzorem je vynásobená velkostí interferenčního obrazce v průzoru. Hologram plní funkci na míru šité difrakční mřížky, která způsobí, že na detektoru vznikne interferenční obrazec, jenž je prakticky stejný jako obrazec scény přes průzor (Obr. 20c). Jinými slovy, světelné pole rekonstruované přes hologram je prakticky stejné jako světelné pole od scény průzorem. Pozorovatel pak neví zda se dívá přímo na scénu přes průzor, nebo vidí jen obraz této scény.

Obr. 21  Rozdílné kmitočty referenčního světla a světla použitého k pořízení hologramu - program holografie.exe

Holografický obraz lze vytvořit také s koherentním světlem, jehož kmitočet je odlišný od toho, kterým byl hologram pořízen. V tom případě pozorovatel zaznamenává obraz nejen odlišné barvy (barvy rekonstrukčního světla), ale také jiných rozměrů. V případě nižšího (vyššího) kmitočtu rekonstrukčního světla než je světlo použité k pořízení hologramu, pozorovatelé zaznamenávají zvětšení (zmenšení) rozměrů virtuálních objektů scény. Hologram se chová jako zvětšovací (zmenšovací) lupa, která zobrazuje rozměry předmětů zvětšené (zmenšené) v poměru zmíněných kmitočtů. Na první pohled tvrzení, že se světlem delší vlnové délky můžeme vidět zvětšený obraz s paralaxem, zní jako paradox. Nicméně je to skutečnost, která v perspektivě díky technologickému pokroku nevylučuje ani možnost záznamu předmětů molekulárních rozměrů (např. X-paprsky) a prohlížení jejich trojrozměrného obrazu viditelným světlem ve zvětšeném měřítku. Tuto vlastnost holografie zde neumíme modelovat počítačem, ale následující úvaha to snad přiblíží.

Máme výkres nějakého objektu, na němž jsou data uváděna v délkové jednotce centimetr L1. Tento výkres je analogií hologramu. Postavíme-li kopii objektu přesně podle těchž údajů, ale podle délkové jednotky L2 (metr nebo milimetr), výsledek bude replika jiných rozměrů než je originální objekt a to v délkovém poměru L2/L1. Je-li L2 > L1 pak i replika je větší než originál, je-li L2 < L1 pak replika je menší. Replika je obdoba holografického obrazu.

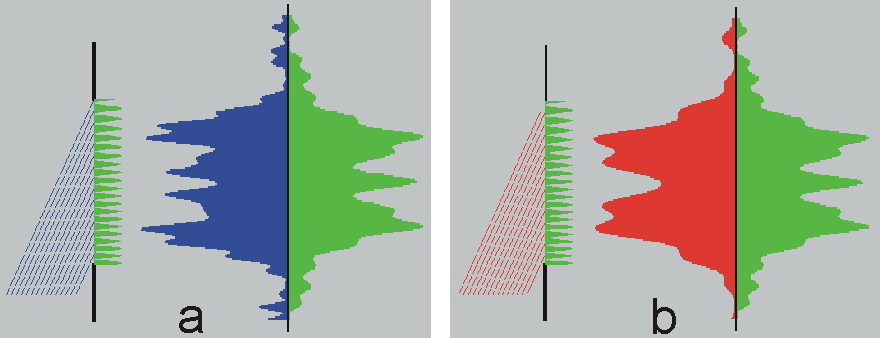
Měřicím nástrojem v holografii je délka, kterou foton uletí za dobu jedné otáčky vektoru – je to vlnová délka světla, která se zkracuje úměrně s růstem kmitočtu světla. Na Obr. 21 je vidět jak se interferenční obrazec změní, když hologram je ozářen světlem vyššího (Obr. 21a) nebo nižšího (Obr. 21b) kmitočtu než je ten, kterým byl hologram pořízen. Z toho podle úvah v předešlém odstavci vyplývá, že velikost virtuálního předmětu rekonstruovaného modrým (červeným) světlem je menší (větší) než je velikost obrazu, který je rekonstruovaný zeleným světlem. Rekonstruované interferenční obrazce mají obdobný tvar, jaký by měly i při rekonstrukci přes hologram „své barvy“ - viz holografie.exe.

I zlomek hologramu poskytuje možnost prohlížet scénu tímto zlomkem, ovšem jakoby přes adekvátně zmenšený průzor. Zlomek hologramu lze totiž chápat jako hologram pořízený při tomto zúženém průzoru. Všechny hologramy na Obr. 20 lze považovat za zlomek většího hologramu.

Holografie nachází uplatnění počínaje uměním, ochranou dokladů, sofistikovanými vědeckými přístroji atd. Holografie se datuje od roku 1947. Objevil ji britsko/maďarský vědec Dennis Gabor ve snaze dosáhnout větší rozlišitelnost dosahovanou elektronovým mikroskopem. Za svůj objev byl Dennis Gabor (původním jménem Gábor Déneš narozený v Budapešti v r. 1900) v roce 1971 poctěn Nobelovou cenou.