Rozptýlené trasy fotonu

Každodenní zkušenost říká, že světlo se šíří přímočaře. Geometrická optika to považuje za jeden svůj postulát, když světelné paprsky znázorňuje jako přímky. Kvantová elektrodynamika však vychází z tvrzení, že světelné účinky na detektoru způsobují fotony. Při výpočtu pravděpodobnosti jejich dopadu na daný bod detektoru, podle Pravidla č. 3, je třeba započítat příspěvky všech možných tras. V souladu s Pravidlem č. 5 máme na mysli jen jeden foton, ale výsledky jsou platné i pro svazek fotonů.

Jenže co to znamená všechny trasy? Nevíme po jaké trase se foton pohybuje. Proč bychom měli Přírodě předpisovat přímočarý let fotonu? Proto tvůrci QED vymysleli metodu výpočtu, která zohledňuje všechny možné trasy za cenu toho, že lze určit jen pravděpodobnost dopadu fotonu na zvolené místo.

Pomocí počítačového programu rozptyl-tras.exe pojednáme o rozptylu tras fotonu, kde se možné trasy modelují nahodile generovanými body zlomu tras po kouskách lineárních. Ukážeme proč lze považovat šíření světla (na rozdíl od fotonu) za přímočaré. Navíc ukážeme jak lze chápat tvrzení, že světlo se v látkovém prostředí šíří menší rychlostí c než je jeho rychlost c₀ ve vakuu, ačkoliv má foton i v látkovém prostředí obvyklou rychlost c₀.

Program respektuje uvedený Princip C a jeho algoritmus splňuje následující zásady:

• Program modeluje trasu fotonu, která vykazuje zlomy v nahodilých bodech. Body zlomu se nahodile generují jak ve směru paralelním se spojnicí zdroje světla s detektorem, tak i ve směru kolmém. Od každého zlomu tak pokračuje trasa nahodilým směrem (Obr. 3a). Počet tras fotonu a počet zlomů lze v programu volit.
  
• Rozptyl bodů zlomů ve vertikálním směru se v 80 krocích zužuje od maximální šíře koridoru směrem ke přímé spojnici mezi zdrojem a detektorem světla až do nulové šířky. A pak se koridor opět rozšiřuje.
  
• Pro každou šířku koridoru a zadaný počet zlomů se individuálně pro každou možnou trasu fotonu vypočítá délka trasy a radiusvektor fotonu po jeho dopadu na detektor. Radiusvektory fotonu v každém koridoru se vektorově sčítají (viz Obr. 3a).
  
• Součtový radiusvektor fotonu pro daný koridor tvoří příspěvek k globálnímu sumárnímu radiusvektoru fotonu ve všech 80 koridorech. Globální sumární radiusvektor je znázorněn uprostřed Obr. 3.

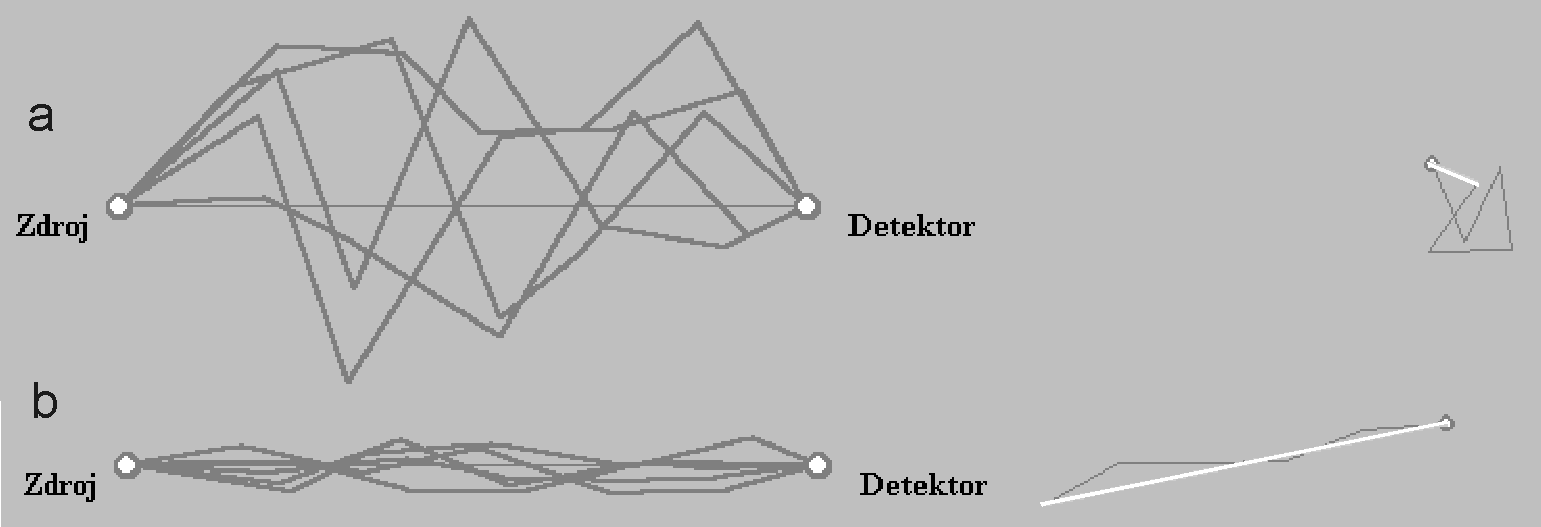
Obr. 3a  Pět možných tras fotonu v koridoru (a široký, b úzký) a součet radiusvektorů
- program mozne-trasy-koridoru.exe

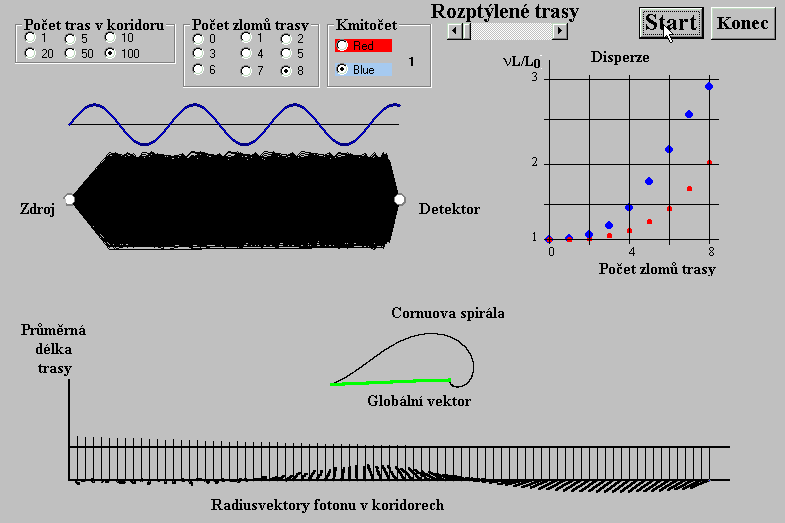
Obr. 3  Rozptyl tras fotonu - program rozptyl-tras.exe

Na Obr. 3 v spodní části jsou vyneseny radiusvektory od nejširšího koridoru k nejužšímu z leva napravo. V širokých koridorech je součet radiusvektorů velmi krátký z toho důvodu, že vektorový součet vektorů je obvykle menší co do hodnoty než je aritmetický součet hodnot jednotlivých vektorů. Proto výsledný radiusvektor fotonu v širokém koridoru jen málo přispívá ke globálnímu sumárnímu vektoru všech koridorů. Navíc součtové vektory v sousedních širokých koridorech mají "rozházené" směry, takže se v globálním vektorovém součtu vektorů částečně ruší.

Na pravé straně seznamu koridorů jsou znázorněny radiusvektory patřící ke koridorům úzce přimykajícím k přímé spojnici zdroje a detektoru světla. Výsledné radiusvektory těchto koridorů jsou nejen dlouhé, ale v jejich širším okolí mají stejný směr. Z toho důvodu právě tyto radiusvektory určují celkovou délku globálního radiusvektoru všech koridorů (Obr. 3).

Z toho plyne závěr, že konečnou délku globálního radiusvektorů určují trasy fotonu, které se s malým rozptylem proplétají v blízkosti přímky mezi zdrojem a detektorem světla. Vzniká tak dojem, že světlo se šíří po přímkových paprscích. Představa o přímkových paprscích je pragmatická představa, která patří nejen k postulátům geometrické optiky, ale akceptuje ji i QED ve snaze zjednodušit kreslení obrázků a usnadnit jejich slovní výklad.

Ve vakuu nejsou žádné překážky (elektrony), které by bránily fotonu v jeho volném letu. Tuto ideu program simuluje nulovým počtem zlomů jeho dráhy. Přímočará trasa mezi zdrojem a detektorem má délku L₀. Se zvyšujícím se počtem zlomů se délka průměrné n_r trasy L prodlužuje a globální vektor se zkracuje vinou rozptýlené trasy. Poměr L/L₀ je materiálová konstanta. Její vynásobení kmitočtem světla se nazývá index lomu n = ν L/L₀ = ν V₀/V, kde V₀ je délka globálního vektoru v nepřítomnosti zlomů, a V v jejich přítomnosti. V učebnicích se index lomu uvádí jako poměr rychlosti světla c₀ ve vakuu k jeho rychlosti c v látce n = c₀/c. Nicméně, foton se i v látce pohybuje rychlostí c₀, jenže po klikaté dráze. A to mu zabere více času.

V diagramu v pravém horním rohu Obr. 3 je vynesený index lomu pro frekvenci modrého a červeného světla. Jedna perioda sinusoidy nad trasami znázorňuje vlnovou délku světla zvolené barvy. Modré světlo má dvakrát vyšší frekvenci než červené, a tudíž jeho vlnová délka je dvakrát kratší. Materiálová konstanta L/L₀ je v grafu zastoupená počtem zlomů trasy. Kmitočtová závislost indexu lomu, nazývaná disperze, se projevuje v rozmanitých formách všude tam kde světlo prochází prostředím s proměnlivým indexem lomu. Její různé projevy simulujeme v dalších oddílech.

Publikované hodnoty indexu lomu se týkají absolutního indexu lomu n_a, když index lomu vakua má hodnotu 1 podle definice. V naši notaci je n_a = νL/L₀ / νL_v/L₀ = L/L_v, kde L_v je průměrná délka trasy fotonu ve vakuu. Odvodili jsme důležitý vztah L = n_aL_v, který využijeme při simulací dějů v souvislosti s disperzi. Pro vodu se uvádí hodnota n_a = 1,33, pro sklo 1,6 až 1,9. Vysokou hodnotu vykazuje diamant n_a = 2,42 a křemík 3,96. Index lomu vzduchu je 1,000239. Germanium je průzračné pro infračervené záření v oblasti mikronových vlnových délek a jeho index lomu je 4. To ho činí vhodným materiálem pro termovizní optiku.

Foton i ve vakuu letí od zdroje světla k detektoru po klikatých cestách, vždyť s jistou pravděpodobností doletí ke každému bodu prostoru. Jelikož absolutní index lomu látky je vyjadřován relativně k vakuu, můžeme počítat s tím, že průměrná délka trasy fotonu ve vakuu se rovná přímé vzdálenosti detektoru od zdroje L_v = L₀.