Difrakce na mřížce

V souvislosti s Obr. 7 v oddílu Zrcadlení jsme uvedli, že části zrcadla vzdálené od detektoru se nezúčastňují, nebo se jen málo zúčastňují na zrcadlení. Je tomu tak proto, že radiusvektory fotonu příslušných drah jsou střídavě orientovány tak, že se ve vektorovém součtu vzájemně ruší. Nicméně trasy fotonu od těchto částí zrcadla také přispívají k efektu zrcadlení a po úpravě zrcadla dokonce mají hlavní podíl na zrcadlení.

Úprava zrcadla spočívá v tom, že zabráníme zrcadlení v těch dílkách zrcadla, pro které je směr radiusvektorů opačný než pro sousední dílky. Zůstanou pak jen radiusvektory, které ukazují prakticky jedním směrem (Obr. 8) a jejich součet dává pěkně dlouhý výsledný radiusvektor. Takto upravené zrcadlo nazýváme difrakční mřížka a jev s tím spojený se jmenuje difrakce na mřížce. S difrakcí (ohybem na štěrbině) jsme se již setkali v oddílu Interference a difrakce na štěrbině.

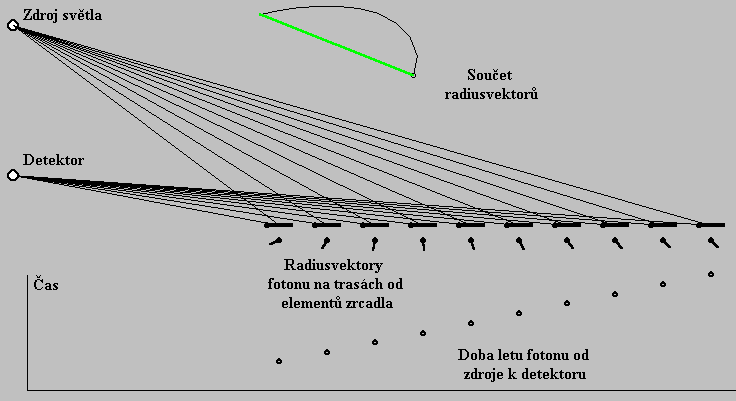
Obr. 8  Difrakce na mřížce - program difrakce-na-mrizce.exe

Difrakční mřížku získáme pravidelnými rýhami (poškrábáním) zrcadla. Takto vzniklá difrakční mřížka funguje jako zrcadlo jen pro světlo (fotony) určitého kmitočtu odpovídajícího rozteči rýh na zrcadle. Pro jiné kmitočty světla difrakční mřížka jako zrcadlo nefunguje. Vyzkoušet si to lze programem difrakce-na-mrizce.exe pro různé kmitočty a porovnat výsledky se zrcadlením obyčejného zrcadla.

Pomocí programu difrakce-na-rostu.exe můžeme fenomén difrakce na mřížce podrobněji analyzovat a sledovat členitost interferenčního obrazce v závislosti na kmitočtu světla a počtu průzorů v mřížce. Interferenční obrazec (pravděpodobnost dopadu fotonu na detektor/stínítko) má periodickou strukturu. Rozestup „balíků“ vysokých hodnot interferenčního obrazce se zvětšuje úměrně se snižováním kmitočtu světla. Interferenční obrazec se svými bočními balíky je svého druhu zvětšený obraz mřížky.

Uvedené vlastnosti difrakce na mřížkách nacházejí využití v technice a ve výzkumu světla a to nejen ve viditelném oboru frekvencí. K nejznámějším aplikacím patří rozklad směsy světla na jeho složky, jak to ilustruje skica v pravém horním rohu Obr. 8a. Kolmo na mřížku dopadá směs tří monochromatických světel barvy červené, zelené a modré. Na stínítku proti mřížce tato směs tvoří bílou barvu. Červené světlo má nižší kmitočet než zelené, nebo modré, a tudíž se vychyluje více a na stínítku má větší odstup od středu mřížky než zbývající dvě barvy.

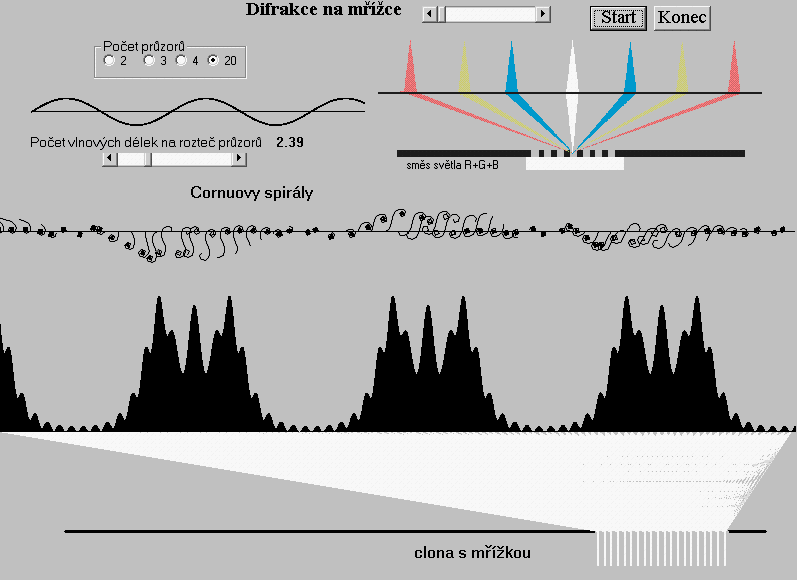
Obr. 8a  Difrakce na mřížce průzoru - program difrakce-na-rostu.exe

Barevné obrazce, které pozorujeme na kompaktním disku (CD) při ozáření slunečním světlem, jsou projevem rozkladu světla difrakcí na mřížce. Jmenovitá rozteč drážek na CD je 1,6 mikrometru. Červené světlo má vlnovou délku v rozsahu 0,6–0,74 a modré světlo 0,435–0,5 mikrometru. Milimetrové rozestupy červeného a modrého konce spektra na CD představují několika 1000× zvětšení rozkroku CD mřížky.

Programem difrakce-na-rostu.exe můžeme sledovat, že se snižováním (zvyšováním) kmitočtu světla ν se vzájemná vzdálenost D balíků vysokých hodnot interferenčního obrazce zvětšuje (snižuje). V programu není implementována možnost měnit rozkrok mřížky d, jelikož všechny tvary interferenčního obrazce se dají předvést volbou kmitočtu ν. Mezi uvedenými veličinami totiž platí jednoduchá úměrnost D = m/(dν), kde m je konstanta vyjadřující vzdálenost mezi mřížkou a detektorem. Tuto závislost lze odvodit elementárním matematickým postupem, nicméně v našem pojednání dáme přednost fyzikálnímu výkladu.

Příroda neměří vzdálenost v lidmi stanovených jednotkách (metr, nanometr), ale ve vlnové délce světla (mluvíme-li v pojmech vlnové teorie) nebo v délce, kterou foton uletí za dobu jednoho cyklu svého kmitočtu ν (mluvíme-li v pojmech fotonové teorie QED). Z toho vyplývá, že při zmenšení (zvětšení) rozkroku mřížky d a při současném zvětšení (zmenšení) kmitočtu ν stejnou mírou se jejich součin nezmění a tudíž rozestup D zůstane taktéž nezměněný.

Budeme-li rozkrok mřížky zmenšovat až do d = 0, namísto mřížky dostaneme jednu širokou štěrbinu, rozestup D bude nekonečně veliký, a interferenční obrazec se zredukuje na jeden balík vysokých hodnot. Tomuto stavu říkáme difrakce na štěrbině, difrakce na apertuře nebo difrakce na hraně. Analýze tohoto druhu difrakce je věnován program difrakce-na-sterbine.exe.