Interference - diskuse

Hloubavý čtenář může namítat, že s reálním interferometrem nelze vytvořit interferenční, difrakční atp. obrazce, pokud zdroj emituje jen jeden foton, jak jsme o tom psali např. v části Interference a difrakce na štěrbině (Obr. 4). V reálném dvojštěrbinovém interferometru proletí foton jednou nebo druhou dírkou clony a dopadne na nahodilý bod detektoru. Z tohoto jediného údaje nelze stanovit pravděpodobnost.

Reální interferometr je v programu interference-diskuse.exe. modelován emitováním fotonů ze zdroje postupně za sebou. Podobně střílí náboje i samopal. Fotony vylétají ze zdroje v nahodilé fázi, proletí nahodile jednou nebo druhou dírkou v cloně a nakonec dopadnou na nahodilý bod detektoru. Emise fotonů pokračuje tak dlouho dokud na všechny body detektoru nedopadne v programu zvolený počet fotonů. Uvedený postupu a jeho výsledky ilustruje Obr. 13 a Obr. 14.

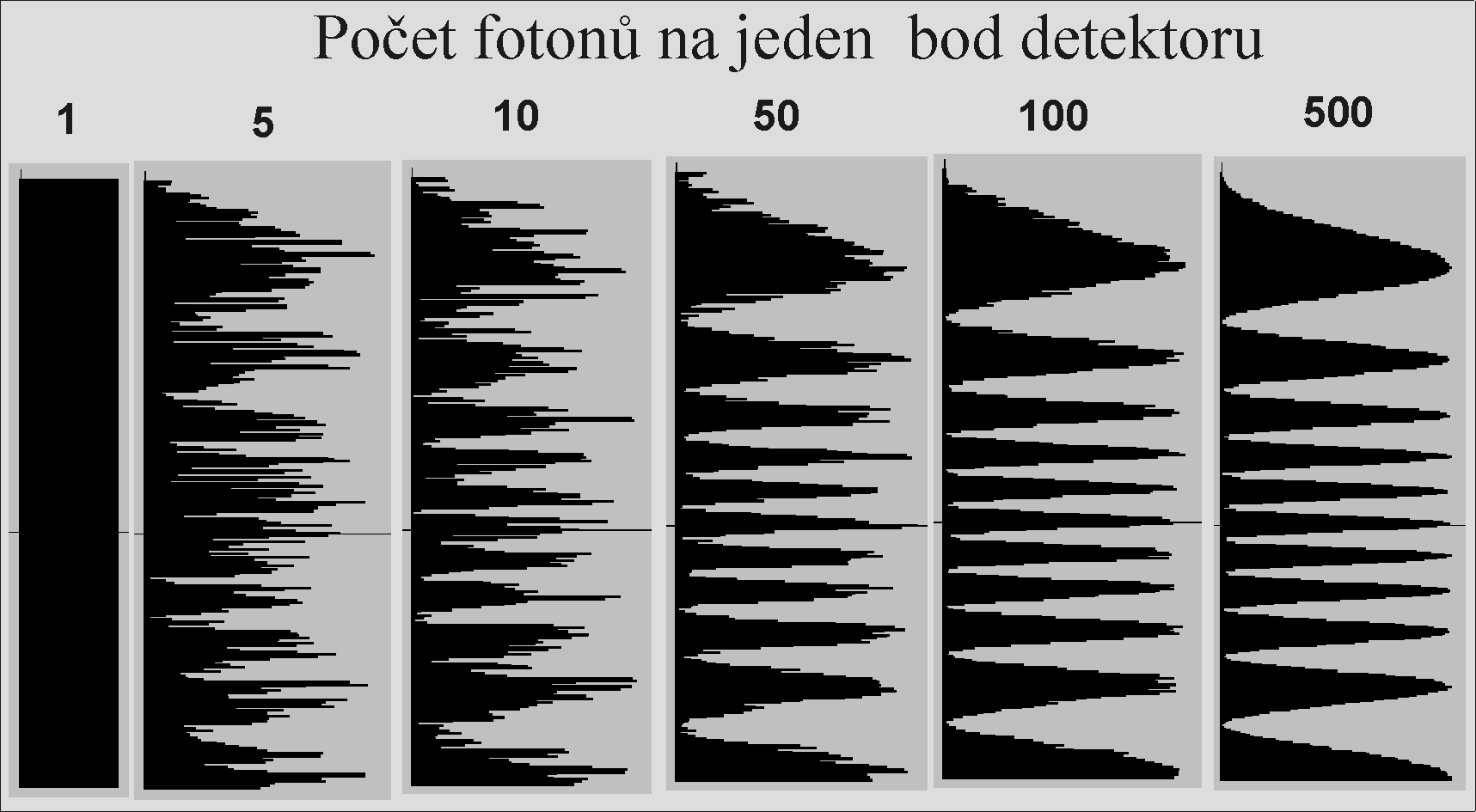
Obr. 13  Interference "palby fotonů" - program interference-diskuse.exe

Na Obr. 13 jsou znázorněny interferenční obrazce (pravděpodobnost) pro různý počet fotonů dopadajících na jednotlivé body detektoru. Dopadá-li na každý bod jenom jeden foton, pak obrazec není členěný, jelikož pravděpodobnost dopadu na každý bod detektoru je stejná. Členitost pravděpodobnosti se začíná projevovat již při pěti fotonech na bod, ale obrazec je výrazně "rozcuchaný". S přibýváním počtu fotonů na bod se interferenční obrazec postupně vyhlazuje. Při počtu cca 500 fotonů na bod dosáhne stejně vyhlazenou podobu jako v oddílu Interference a difrakce na štěrbině (Obr. 4).

Počítačový model ukazuje, že pravidla výpočtu pravděpodobnosti dopadu fotonu na vybrané místo detektoru zohledňují statistické výsledky dopadu mnohočetních fotonů. Tyto výsledky jsou pak vztaženy na jeden foton. Analogicky je to s pravděpodobností P vypadnutí zvoleného čísla při jednorázovém hodu kostkou. Akceptujeme, že tato pravděpodobnost je P = 1/6 na základě statistiky získané mnohonásobným hodem kostkou.

Výše popsaný model vzniku interferenčních obrazců není ve shodě s realitou v tom, že předpokládá součinnost (sčítání radiusvektorů) za sebou "střílených" fotonů. Tento nesoulad se projevuje na Obr. 13 zejména na nečleněném interferenčním obrazci pro jeden foton. Experimenty ukazují, že členěný interferenční obrazec vzniká i tehdy, když fotony se vystřelují za sebou s velkou časovou prodlevou, a tudíž jejích vzájemné ovlivnění nepřichází v úvahu. Vysvětlení podle QED spočívá v tom, že každý foton proletí oběma štěrbinami nedělitelně. Tento neobvyklý pohled, odporující každodenní představě, komentujeme v oddílu Interference a difrakce na štěrbině.

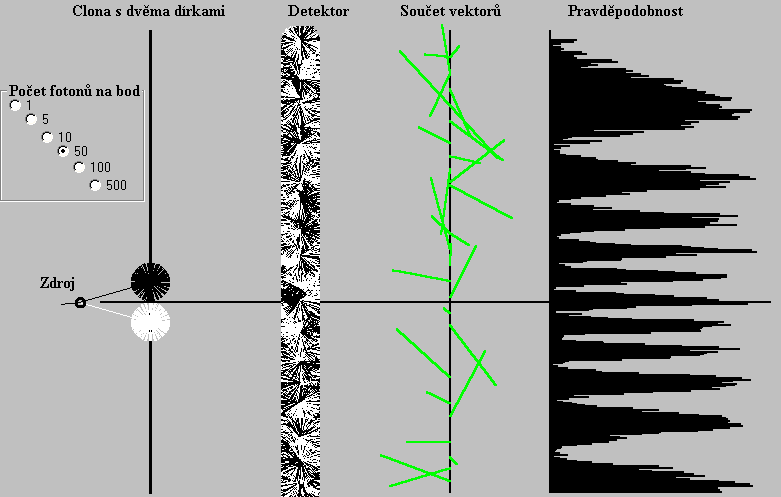
Obr. 14  Dvojštěrbinový interferometr emitující zvolený počet fotonů na bod. Součtové vektory se zobrazují jen v nahodile vybraných bodech detektoru kvůli přehlednosti - program interference-diskuse.exe

Vyhlazování interferenčního obrazce se zvyšujícím se počtem fotonů na bod detektoru se děje v důsledku klesající váhy "výstřelků" nahodilých procesů. Tvar interferenčního obrazce se nakonec shoduje s tvarem získaným pro jediný foton podle pravidel uváděných v oddílu Pravidla výpočtu. Tato shoda, ač jde o rozdílné postupy vyčíslení pravděpodobnosti, má svoje kořeny v zákonitostech velkého počtu nahodilých čísel. Při velkém počtu v průměru přes jednu a druhou dírku proletí stejný počet fotonů, a tudíž v průměru fotony absolvují ty samé trasy, kterými se podle citovaných pravidel počítá pro jeden foton. Na průměrné hodnotě fáze radiusvektorů v okamihu emise fotonů nezáleží, jelikož tato ovlivní jenom směr sumárních radiusvektorů v bodech detektoru. A pravděpodobnost je úměrná kvadrátu hodnoty (délky) sumárního radiusvektoru bez ohledu na jeho směr.

Na Obr. 14a je znázorněna pravděpodobnost dopadu jednoho fotonu na dané místo detektoru. Jelikož foton se nemění se vzdáleností místa dopadu od zdroje, pravděpodobnostní obrazec se rozprostírá do nekonečna. Interferometry však na stínítku registrují interferenci světla v podobě proužků jasu a registrují tak hustotu dopadajících fotonů - počet fotonů na jednotku plochy za sekundu. Hustota fotonů je závislá na vzdálenosti místa dopadu od zdroje, proto interferenční obrazec jasu je prostorově omezen (Obr. 14a).

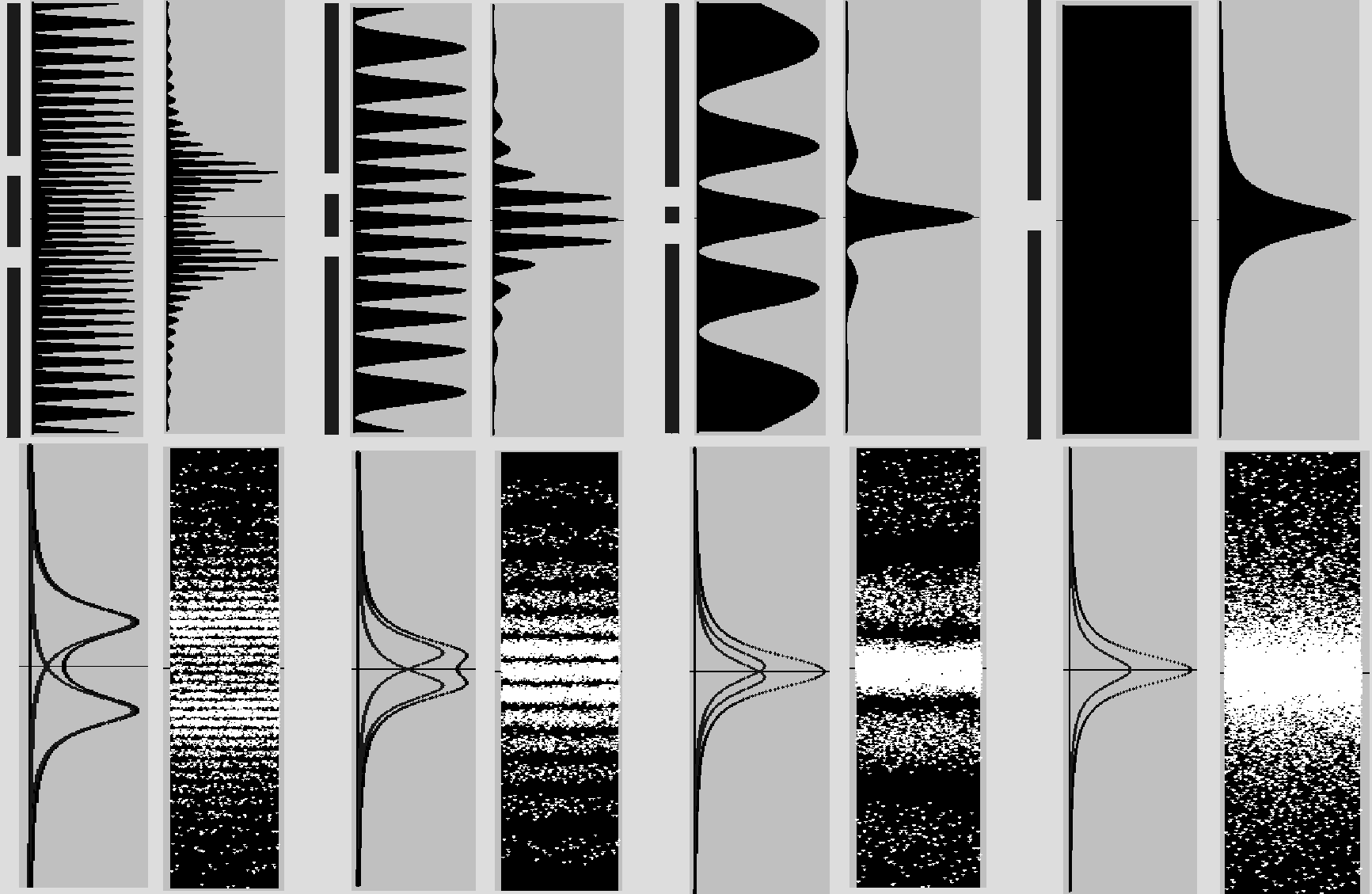
Obr. 14a  Pravděpodobnostní a interferenční obrazce fotonu resp. světla v závislosti na rozteči dírek clony při nezměněném kmitočtu fotonu - program interference-svetla.exe

Chceme-li počítačem modelovat interferenci světla, musíme mezi pravidla výpočtu zakomponovat závislost hustoty fotonů na vzdálenosti R místa detektoru od jedné resp. druhé dírky clony. Interferenční obrazec světla pak vychází jako součin pravděpodobnosti dopadu fotonu a hustoty fotonů v daném místě. Jelikož se fotony šíří rovnoměrně ve všech směrech a plocha koule se středem na dírce je úměrná R², hustota fotonů v místě detektoru je úměrná součtu (1/R²)_A + (1/R²)_B od jedné a druhé dírky. Ve spodní části Obr. 14a jsou znázorněny grafy hustoty fotonů pro jednotlivé rozteče dírek clony, které spolu s ostatními grafy - počínaje pravděpodobnosti dopadu fotonů - tvoří milníky ke konečné ilustraci interference světla hustotou nahodilých dopadů fotonů na stínítko.