Interference a difrakce na štěrbině

Jeden z postulátů geometrické optiky, založené na představě světla jako letící Newtonovy korpuskule, říká o vzájemném nezávislosti paprsků světla. Geometrická optika tak nemůže objasnit vznik jevu, který se jmenuje interference. Naproti tomu, tento jev objasňuje vlnová teorie světla. Pomocí počítačového programu interference.exe na experimentu s dvojštěrbinovou clonou ukážeme jak pojímá interferenci světla kvantová elektrodynamika.

Obr. 4  Dvojštěrbinový interferometr - programy interference.exe a detail-interference.exe

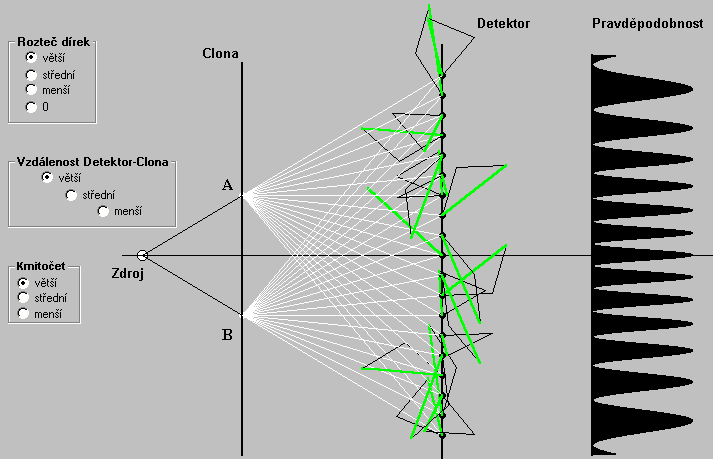
Na Obr. 4 je skica dvojštěrbinového interferometru. Jeho tři hlavní mechanické komponenty jsou: zdroj monochromatického světla (fotonů), clona s dvěma velmi malými dírkami (menšími než setina milimetru pro viditelné světlo), liniový detektor (sada detektorů v řadě). Ze zdroje světla běžně vylétá nespočetné množství fotonů, ale jen některým se poštěstí proletět jednou z dírek a dopadnout na detektor. V počítačovém programu interference.exe sledujeme jeden foton, který nakonec šťastně dopadne na detektor.

Foton proletí přes jednu z dírek A a B. Nezjišťujeme přes kterou. Víme jen, že je to buď dírka A nebo B. Jelikož přesnou polohu dírek známe, je přesně definována také poloha průletu fotonu. Kam poletí foton, co prolétl dírkou, a na které místo detektoru dopadne, to principiálně neumíme předpovědět. Umíme jenom spočítat pravděpodobnost dopadu na předem učené místo D detektoru.

Mezi zdrojem světla a bodem D detektoru přes dírky A a B je nekonečné množství možných tras, kterými by foton mohl letět. Pro všechny trasy by bylo třeba vypočítat radiusvektor fotonu po dopadu a všechny radiusvektory vektorově sečíst. Podle analýzy v předešlém oddílu - Rozptýlené trasy fotonu - naštěstí víme, že výslednou dráhu všech možných tras lze modelovat přímkami zvaným paprsek světla. Díky tomu vystačíme s výpočtem součtu radiusvektorů jenom podél dvou paprscích: od zdroje k dírce A resp. B a odtud k bodu D detektoru.

Na Obr. 4 jsou znázorněny paprsky od dírek A a B k vybraným bodům D na detektoru. Tamtéž jsou znázorněny dva radiusvektory fotonu a jejich vektorový součet. Kvadrát délky součtového radiusvektoru je úměrný pravděpodobnosti dopadu fotonu na daný bod D detektoru. Pro všechny body D detektoru je pravděpodobnost dopadu znázorněn na ose v pravé části Obr. 4.

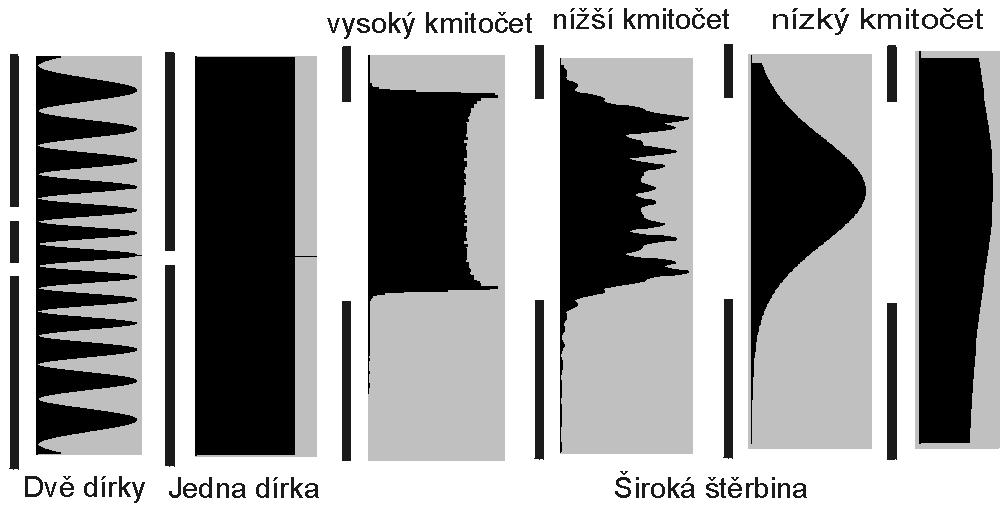
Diagram pravděpodobností vytváří tzv. interferenční obrazec. Podstatné je, že na některé body D detektoru foton má jen mizivou až nulovou šanci dopadnout. Programem interference.exe lze vytvářet interferenční obrazce při různých podmínkách: vzdálenosti detektoru od clony, kmitočtu fotonu (světla), rozteče dírek. Při nulové vzájemné vzdálenosti dírek, kdy obě splynou a na cloně je jenom jedna dírka, členitost obrazce zanikne (Obr. 5).

V kvantové elektronice se pracuje s pojmy teorie pravděpodobnosti a při vyhodnocování experimentů třeba dodržovat její podmínky. V případě clony s dvěma dírkami foton prochází jednou z nich. Nevíme kterou. Proto při výpočtu pravděpodobnosti jeho dopadu na detektor D musíme počítat s oběma možnostmi. Analogický je učebnicový příklad, kdy se hází kostkou a ptáme se, jaká je pravděpodobnost vypadnutí šestky nebo dvojky. Výsledek výpočtu se skládá ze součtu pravděpodobnosti vypadnutí šestky a pravděpodobnosti vypadnutí dvojky. I v případě fotonu se ptáme jaká je pravděpodobnost jeho průletu jednou nebo druhou dírkou. Odpověď je součet pravděpodobnosti průletu jednou dírkou a pravděpodobnosti průletu druhou dírkou. Jenže nyní se podle Pravidla č. 3 jedná o vektorový součet, jehož kvadrát amplitudy je úměrný pravděpodobnosti (program suma-sin.exe). Podstatné je, že stále jde o jeden a tentýž foton, o němž nevíme, kterou dírkou prolétl, a proto počítáme s oběma možnými trasami.

Řekne-li se, že foton proletí jednou nebo druhou dírkou, tak je to mluva poplatná představě fotonu jako kuličky, která může proletět jen jednou štěrbinou. Výklad dějů podle QED však konstatuje, že jeden jediný foton letí všemi možnými trasami a tudíž může proletět i dvěma štěrbinami nedělitelně jak to ilustruje program detail-interference.exe. Pokud se nám toto zdá jako příliš bizarní názor, pak je tomu tak proto, že naše představy o přirozeném chování se vyvinuly na základě každodenní zkušenosti v našem pozemském světě, který v časovém, prostorovém a hmotnostním měřítku není ani velký (v porovnání s vesmírem) ani malý (v porovnání s atomem). Kromě tohoto našeho světa ovšem existuje i kosmický svět obrovských a mikrosvět atomárních rozměrů, a musíme připustit, že v nich se odehrávají děje podle nám nezvyklých pravidel. QED neříká jak se foton v mikrosvětě pohybuje, jen formuluje pravidla pro výpočet pravděpodobnosti výsledků jeho pohybu.

Obr. 5  Souvislost štěrbin clony a interferenčních obrazců

Kdybychom chtěli mermomocí zjistit, kterou dírkou foton proletí, museli bychom za dírkou A umístit detektor D_A a za dírkou B detektor D_B. Proletí-li foton dírkou A, zaregistruje ho detektor D_A. Proletí-li dírkou B, zaregistruje ho detektor D_B. Registrace však není současná, jelikož foton se nemůže rozdvojit, a tudíž detektory registrují různé fotony. Z pohledu výpočtu pravděpodobnosti se zde jedná o dva koncové stavy: registrace události detektorem D_A a registrace jiné události detektorem D_B. Výsledek je interferenční obrazec bez členitosti jako při průletu fotonu jednou dírkou (Obr. 5).

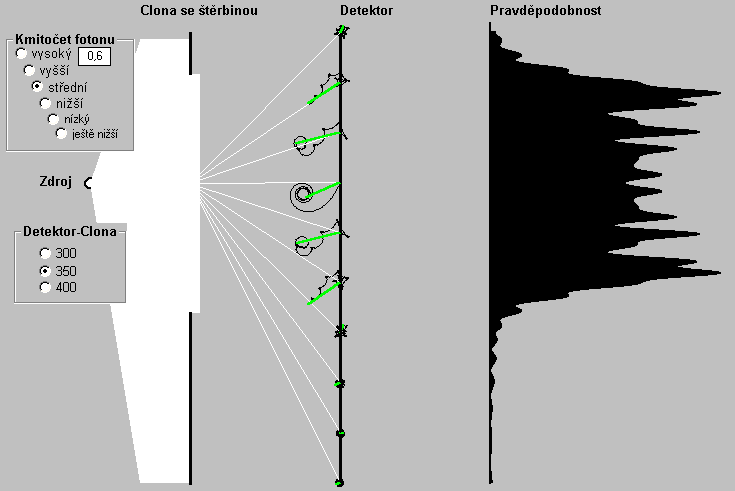
Na Obr. 6 je znázorněn interferenční obrazec od jedné široké štěrbiny. Jelikož štěrbina je široká, ke každému bodu D detektoru vede nespočet paprsků od štěrbiny. Na Obr. 6 kvůli přehlednosti jsou znázorněny jen paprsky ze středu štěrbiny k vybraným bodům D detektoru. Tu je ukázán také součet radiusvektorů po trasách od "všech" bodů štěrbiny. Kvadráty délek součtových vektorů jsou do grafu pravděpodobností vyneseny v pravé části Obr. 6.

Graf pravděpodobností na Obr. 6 zobrazuje jev zvaný difrakce na štěrbině (ohyb na štěrbině). Graf se vyznačuje tím, že v oblasti, která svou šíří odpovídá zhruba rozměrům štěrbiny, je pravděpodobnost dopadu fotonu vysoká. Mimo tuto oblast pravděpodobnost prudce klesá. Tímto poklesem až k zániku se graf difrakce na štěrbině zásadně liší od interferenčních obrazců dírek, kteréžto obrazce mají teoreticky neomezenou šíři. Difrakci je ještě věnován oddíl Difrakce na mřížce.

Graf vykazuje členitost v oblasti s vysokou pravděpodobností a také mimo tuto oblast. Se zvyšováním kmitočtu fotonů se členitost zjemňuje a oblast vysoké pravděpodobnosti se výrazněji vymezuje strmějšími hranami. Při snižování kmitočtu se difrakční obrazec blíží k obrazci pro malou dírku, jelikož šířka štěrbiny se zmenšuje relativně k délce dráhy, kterou foton urazí za jednu sekundu (Obr. 5). Vše lze znázornit pomocí programu difrakce-na-sterbine.exe.

Obr. 6  Difrakce na štěrbině - program difrakce-na-sterbine.exe

Poloha průchodu fotonu clonou a poloha dopadu fotonu na detektor jsou dvě veličiny, které vzájemně souvisí s daným jevem. Podobná vzájemně úzce související dvě veličiny se označují přívlastkem konjugované. Pravděpodobnostní grafy (Obr. 5) ilustrují princip neurčitosti pro interferenci světla. Obecná formulace principu neurčitosti říká, že čím přesněji určíme jednu z konjugovaných veličin, tím méně přesně lze určit druhou. V kvantové fyzice nejznámější je Heisenbergův princip neurčitosti, kde konjugované veličiny jsou poloha a hybnost kvantové částice. Přesným měřením polohy částice narušíme její hybnost, kterou pak již nelze přesně zjistit v její původní velikosti.

V pokusu s interferencí světla od dvou (jedné) dírek v cloně je místo průchodu fotonu clonou přesně definováno, a tudíž místo dopadu na detektor nelze přesně určit, jak to dokládá interferenční obrazec "neomezené" šířky. Naopak s jednou širokou štěrbinou v cloně, která nedefinuje přesně místo kudy foton prochází, souvisí zřetelně ohraničená oblast vysoké pravděpodobnosti dopadu fotonu na detektor. Feynmanova metoda výpočtu pravděpodobnosti sama o sobě respektuje princip neurčitosti aniž by ho bylo třeba zavést jako zvláštní postulát.