Index lomu a rychlost fotonu

Z Maxwellových rovnic pro rychlost c₀ šíření elektromagnetických vln ve vakuu vyplývá vzorec c₀ = (µ₀ε₀)^-1/2, kde µ₀ a ε₀ jsou permeabilita resp. permitivita vakua. Maxwellovy rovnice a z nich vyplývající důsledky jsou exaktně platné jen pro vakuum. Aby se tyto rovnice "zachránily" i pro látkové prostředí, zavádějí se empirické látkové koeficienty relativní permeability resp. permitivity µ_r a ε_r. S nimi vychází rychlost c elektromagnetických vln c = (µ_rε_r))^-1/2 (µ₀ε₀₎)^-1/2. Pro index lomu tak dostáváme vzorec n = c₀/c = (µ_rε_r))^1/2.

Pro vodu např. je µ_r = 1 a ε_r = 81. Teoretická hodnota indexu lomu tak vychází n = 9, ale experimentální hodnota je n = 1,33. Značný rozdíl mezi teoretickou a experimentální hodnotou je důvod, abychom hledali vysvětlení. Rozdíl má svůj původ

• v neodůvodněné extrapolaci ε_r do oblasti světla,
  pro kterou tato experimentální konstanta nebyla zavedena,
  
• v chápání rychlosti c₀ a c.

Tab. 1  Empirické hodnoty

Látka	index lomu n=c0/c	εr	µr	Poznámka
Vakuum	1	1	1	z definice
Vzduch	~1,00029	~1	~ 1
Voda	~1,333	~81	~ 1
Led	~1,31	~4,8	~ 1
Oleje	1,478–1,505	5,5–5,8	~ 1
Skla	1,515–1,752	3,8–19	~ 1
Diamant	~2,417

Zavedení pojmu relativní permitivity ε_r objasníme pomocí Obr. 15. Mezi dvěma elektrodami se nachází dielektrikum reprezentované svými dipóly. Větší kolečka na Obr. 15a,b představují tzv. volné náboje přivedené k elektrodám ze zdroje napětí V. Dipóly jsou reprezentovány menšími kolečky, které jsou polarizovány (natočeny) pod plivem volných nábojů. V hloubi těla dielektrika se působení dipólů vzájemně ruší a k intenzitě elektrického pole E přispívají jenom tzv. vázané náboje (Obr. 15b). Jsou to náboje, které nemají sousední dipól ze strany elektrod.

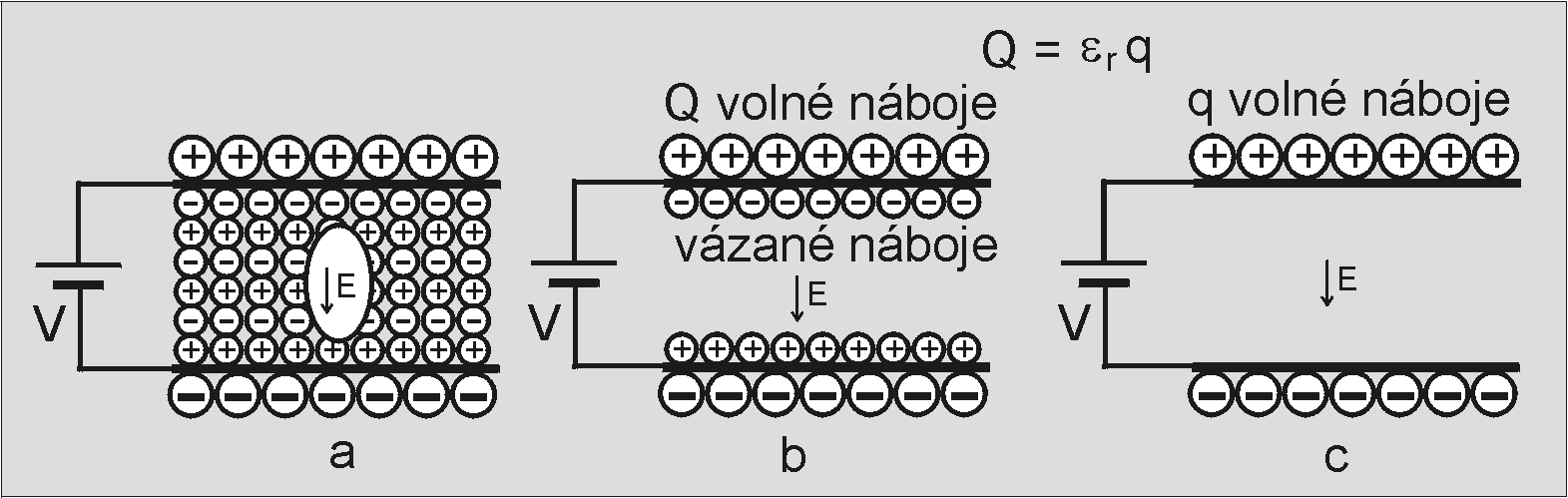
Obr. 15  K vysvětlení pojmu relativní permitivity

Jelikož vázané náboje zeslabují účinky volných nábojů Q, je velikost Q větší, než by byla velikost volných nábojů q v nepřítomnosti dielektrika (Obr. 15). Látková konstanta relativní permitivity vyjadřuje poměr uvedených volných nábojů: ε_r = Q/q. Relativní permitivita je významná látková konstanta z pohledu kondenzátorů, avšak její aplikace pro výklad šíření elektromagnetických vln a indexu lomu je neodůvodněnou extrapolací.

Obvyklou rychlostí fotonů se rozumí rychlost světla c₀ měřená ve vakuu. V látkovém prostředí trasa fotonu je klikatá vlivem jeho rozptylu elektrony. Tím se zvětší průměrná délka doby putování fotonu mezi zdrojem a detektorem - viz oddíl Rozptýlené trasy fotonu. To se pak jeví jako snížená rychlost světla na hodnotu c v látkovém prostředí.

Na závěr je třeba říci, proč platí vztah c₀ = (µ₀ε₀)^-1/2 pro vakuum exaktně. Odpověď je jednoduchá. Protože tak bylo stanoveno na základě následujících rozhodnutí**:

1. Mezinárodní komise pro váhy a míry doporučila v roce 1948 používat soustavu jednotek SI (Systeme Internadional d'unités), která byla u nás uzákoněna Sbírkou zákonů 35/62. Podle této soustavy je jednotka proudu ampér A základní měrnou jednotkou podle následující definice:
   Jeden ampér je proud, který při stálém průtoku dvěma rovnoběžnými přímkovými vodiči zanedbatelného kruhového průřezu, umístěnými ve vakuu ve vzdálenosti r = 1 m, vyvolá mezi vodiči sílu F = 2.10^–7 newtonu na L = 1 m délky vodiče.
2. Je uzákoněno používat racionalizovanou formu Maxwellových rovnic a zákonů elektromagnetického pole. Pro permeabilitu vakua tak vyplývá hodnota µ₀ = 4π.10^-7 [mkgs^-2A^–2], kterou z Ampèreova zákona F = µ₀I₁I₂L(2πr)^–1 dostaneme když sem dosadíme velikost proměnných z výše uvedené definice jednotky ampér.
   
3. Hodnota permitivity se vypočítá ze vztahu pro rychlost c₀ = (µ₀ε₀)^-1/2, kde c₀ je obvyklá rychlost světla ve vakuu.
   

Permitivita a permeabilita nejsou přirozené veličiny Přírody, nýbrž konstanty subjektivně zvolených jednotek a formy Maxwellových rovnic. Jenom součin µ₀ε₀ je přirozenou veličinou Přírody danou rychlostí světla c₀ = (µ₀ε₀)^-1/2 ve vakuu.

 

**
Ladislav Szántó: Maxwellovy rovnice a jejich názorné odvození
Nakladatelství BEN - technická literatura, Praha, 2003