Rozptyl fotonu elektrony

Model neobyčejného chování světla na tenkém sklíčku, který je uveden v předešlém oddílu Dvojodraz, umožňuje stanovit pravděpodobnost dopadu fotonu na detektor ve shodě s experimenty. Nicméně model je založen na nesprávné intuitivní představě o jevu, podle něhož k částečnému odrazu světla dochází jen na rozhraní sklíčka a vzduchu. Proč by se měl foton (světlo) odrážet jen od dvou rozhraní sklíčka? Ve skutečnosti k odrazům fotonu dochází i v objemu sklíčka.

V tomto oddílu se podíváme na neobyčejné chování světla na základě fyzikálně lépe podložené představy o podstatě dějů ve sklíčku. Jedná se o rozptyl fotonu elektrony. Lehounce se tím dotkneme druhé části Feynmanovy knihy Neobyčejná teorie světla a látky.

Elektrony jsou neuspořádaně rozházeny po celém objemu sklíčka. Nicméně, ve snaze zjednodušit výpočty předpokládejme, že elektrony jsou rozloženy po řádcích, jak to znázorňuji horizontální linie sklíčka na Obr. 11. Při výpočtu pravděpodobnosti dopadu fotonu na detektor postupujeme v programu rozptyl-fotonu-elektrony.exe tak, že s možnými trasami fotonu počítáme nejdřív k elektronům v nejvyšší linii, a pak postupně k dalším níže položeným liniím. Výpočet je dále zjednodušen tím, že se využijí výsledky analýzy prezentované v oddílu Zrcadlení: k výslední pravděpodobnosti nejvíc přispívá radiusvektor fotonu s nejkratší dobou letu od zdroje k elektronu a odtud k detektoru. Jen s těmito trasami, pro něž je úhel dopadu na linii elektronů rovný uhlu odrazu, se v programu počítá.

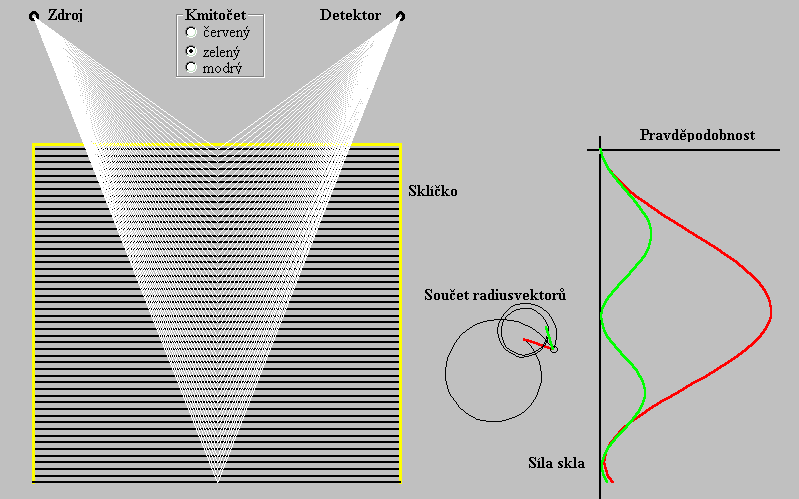
Obr. 11  Rozptyl fotonu elektrony - program rozptyl-fotonu-elektrony.exe

Na Obr. 11 je graf pravděpodobnosti dopadu rozptýleného fotonu na detektor znázorněn pro dva kmitočty fotonu: pro nižší kmitočet (červený okraj viditelného spektra) a pro vyšší kmitočet (zelená část viditelného spektra). V prostřední části Obr. 11 jsou uvedeny součty radiusvektorů pro nižší resp. vyšší kmitočet fotonu. Při vyšším kmitočtu fotonu se radiusvektor víc otočí než při nižším kmitočtu na té samé dráze. Proto je sumarizační křivka vyšších kmitočtů víc zakřivena, a tudíž rozměrově menší. V důsledku toho i maximální hodnota pravděpodobnosti je menší. Připomínáme, že hodnota pravděpodobnosti je úměrná kvadrátu délky radiusvektoru.

Při přesnější analýze rozptylu fotonů elektrony v těle sklíčka (Obr. 11) má pravděpodobnost dopadu fotonu na detektor periodický průběh v závislosti na síle sklíčka. Podobný průběh má pravděpodobnost i při zjednodušené analýze jevu, kdy se předpokládá odraz fotonu jen od dvou rozhraních sklíčka se vzduchem (Obr. 10). Nicméně velký rozdíl mezi nimi spočívá v tom, že maximální hodnota pravděpodobnosti při přesnější analýze závisí na kmitočtu fotonu (světla), zatím co při zjednodušené analýze nikoli. Vysvětluje se to tím, že při dvojodrazu je hodnota vektorového součtu dvou vektorů při určité síle sklíčka rovna algebraickému součtu hodnot jednotlivých vektorů nezávisle na kmitočtu fotonu. Při rozptylu fotonu na mřížce elektronů rovnost tohoto druhu nemůže nastat.