Parabolické zrcadlo

Parabolické zrcadlo je nepostradatelným dílem mnoha optických přístrojů. Jelikož světlo je jistá forma elektromagnetického záření, funguje parabolické zrcadlo i jako anténa telekomunikačních spojů. Jen její rozměry třeba navrhnout přiměřeně vlnové délce elektromagnetického záření.

Bílé přímky na Obr. 18 představují paprsky světla. Na parabolické zrcadlo dopadá plošná vlna a její paprsky souběžné s optickou osou se odrážejí od parabolického zrcadla. Podle jednoho postulátu geometrické optiky úhel dopadu paprsku se rovná úhlu odrazu, přičemž úhel se měří vzhledem k tečně paraboly v místě dopadu. Bod na optické ose kde se odražené paprsky křižují se nazývá fokus (ohnisko) paraboly. Jelikož se všechny odražené paprsky střetávají na ose v jednom bodě, ohnisková vzdálenost nezávisí na apertuře (otvoru clony) paraboly. V tomto ohledu je parabola optimální tvar zrcadla. Rozložení světla v okolí fokusu geometrická optika neřeší.

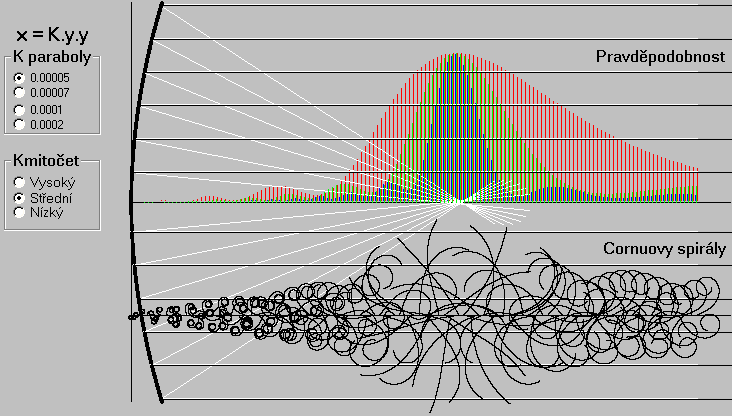
Obr. 18  Obrazce pravděpodobnosti pro kmitočet Nízký (široký graf), Střední, Vysoký
  - program parabola.exe

Jiná je situace z pohledu kvantové elektrodynamiky QED. Na Obr. 18 černými liniemi jsou zobrazeny reprezentativní trasy fotonu jen v úsecích před dopadem na zrcadlo. Trasy po odrazu mezi zrcadlem a body na optické ose si lze domyslet. Fokus parabolického zrcadla je bod na jeho optické ose, v němž pravděpodobnost dopadu fotonu vykazuje maximální hodnotu.

Na Obr. 18 jsou znázorněny tři obrazce pravděpodobnosti dopadu fotonu v závislosti na jeho kmitočtu. Dopadající foton i po odrazu se stále pohybuje ve stejném prostředí. V důsledku toho se neprojevuje efekt disperze světla a poloha fokusu (na rozdíl od ohniskové vzdálenosti lupy - viz oddíl Lupa) se neposouvá s kmitočtem fotonu (světla). Obrazec pravděpodobnosti se ovšem rozšiřuje s klesající kmitočtem fotonu.

Na Obr. 18 jsou znázorněny také Cornuovy spirály. V okolí fokusu už nepřipomínají spirály s typicky zakroucenými očky na konci, ale blíží se k přímce. Pravděpodobnostní obrazce a tudíž i poloha fokusu byly vypočítány metodou vektorového součtu radiusvektorů po všech reprezentativních trasách fotonu. Takto určená poloha fokusu souhlasí s polohou určenou podle postulátu odrazu geometrické optiky, jehož správnost se tímto jenom potvrzuje. Parabola je definována rovnicí x = Ky² s parametrem K, který v programu parabola.exe je volitelný. Parametr K určuje tvar paraboly a tudíž i její ohniskovou vzdálenost. S větší hodnotou K se ohnisková vzdálenost zmenšuje a šíře pravděpodobnostního obrazec se zužuje.