Pravidla výpočtu

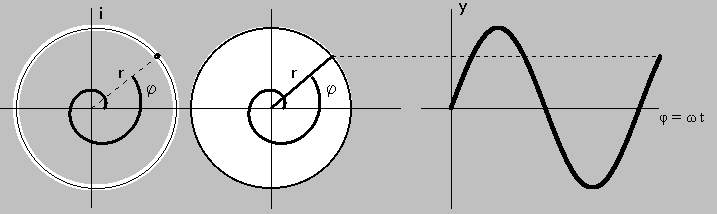
Foton je v teorii QED nositelem světla (nejmenší částice elektromagnetického pole), jehož energie je úměrná kmitočtu ν světla. Řekne-li se kmitočet, má se na mysli kmitání, které se dá matematicky popsat sinusovou funkcí. Na pravé straně Obr.1 je zobrazena jedna perioda a něco sinusoidy v kartézských souřadnicích.

Obr. 1  Tři reprezentace sinusoidy: komplexním číslem, radiusvektorem a kartézskými souřadnicemi
- program sinusoida.exe.

V zde uváděné teorii je podstatná reprezentace sinusoidy rotujícím radiusvektorem (Feynman mluví o ručičce stopek), kde r představuje amplitudu sinusoidy a úhel φ její fázi.

Převod radiusvektorové reprezentace sinusoidy na reprezentaci v kartézských souřadnicích vyjadřuje rovnice y = r.sinφ. Reprezentace radiusvektorem se použije tam, kde se jedná o sčítání sinusoid při paralelním působení dějů. Součet dvou nebo více sinusoid je dán vektorovým součtem jejich radiusvektorů. Součet sinusoid resp. jejich radiusvektorů stejného kmitočtu je opět sinusoida, jejíž amplituda se rovná délce součtového radiusvektoru - program suma-sin.exe.

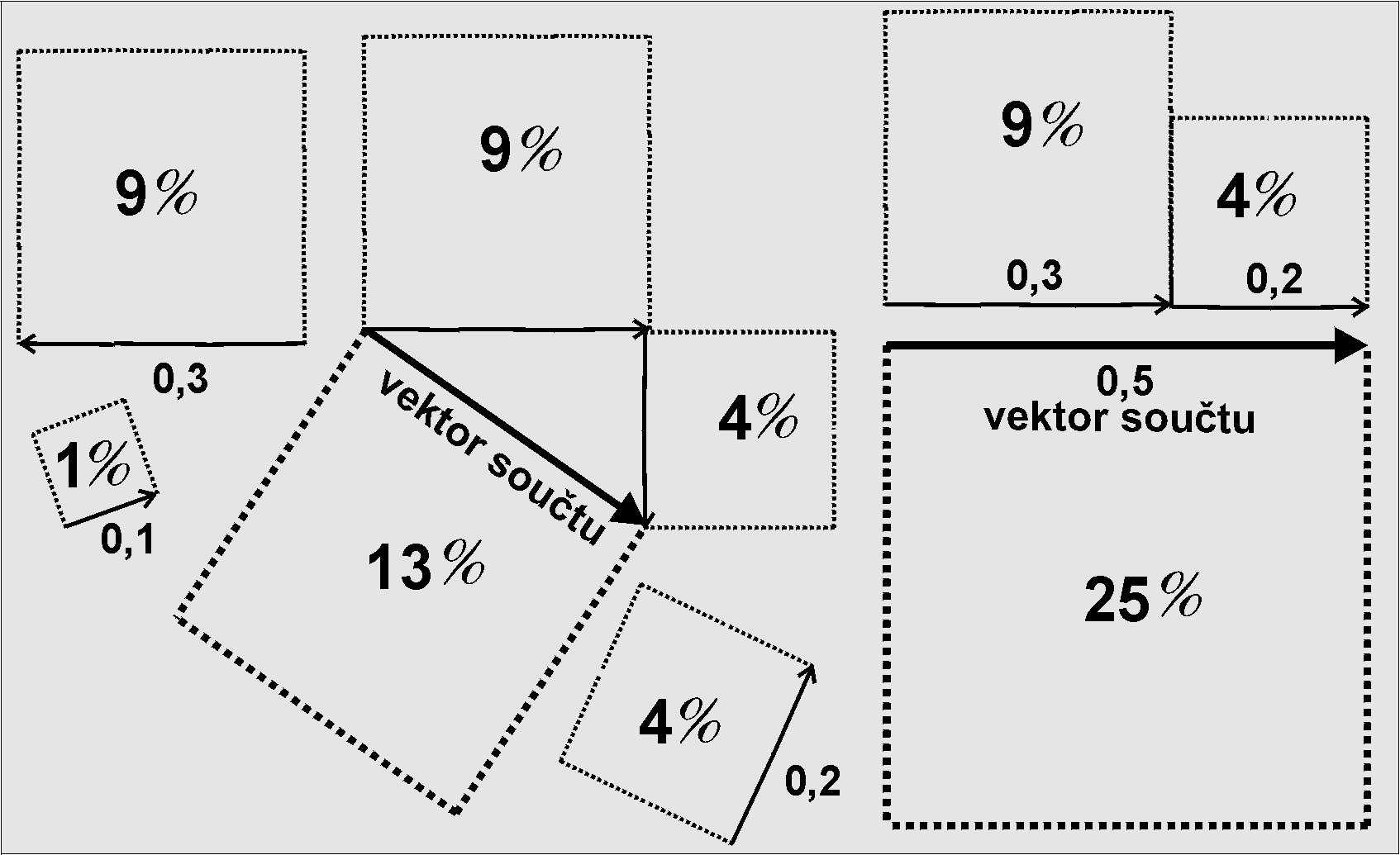
Obr. 2  Radiusvektory a pravděpodobnost, kterou reprezentují

Reprezentace sinusoidy komplexním číslem je založena na Eulerovém vzorci: r e^{i φ} = r (cos φ + i sin φ), kde sinusoidu představuje imaginární část komplexního čísla. Jelikož sinusoida je vyjádřena exponenciální funkcí, Eulerův vzorec se s výhodou použije tam, kde se jedná o násobení sinusoid při sériovém působení dějů. Výsledek násobení dvou a více exponenciálních funkcí je exponenciální funkce, jejíž hodnota se rovná násobku amplitud jednotlivých sinusoid a její fáze součtu fází jednotlivých sinusoid.

Níže uvedeme pravidla, jimiž se řídí výpočty v počítačových programech. Ptáte-li se, proč jsou některé z nich tak neočekávané, pak odpověď je jednoduchá. Protože jsou součástí objevu. Objevu, který umožňuje dosáhnout výsledky výpočtů, které se shodují s experimentálním pozorováním. Souhrnem lze říci, že pravidla konkretizují následující úvahu. Nevíme, jakou trasou foton letí od zdroje k zvolenému cíly (k detektoru). Proto musíme vzít do úvahy všechny myslitelné trasy a slevit z našich požadavků. Neumíme vypočítat, zda foton doletí na zvolené místo. Musíme se spokojit jen s výpočtem pravděpodobnosti jeho dopadu na určený bod. Pak už jen zbývá objevit postup výpočtu, který započítává všechny myslitelné trasy (nebo jejich reprezentantivní vzorky) a dává výsledek shodný s pozorováním. Pravidla jsou podkladem k algoritmu tohoto výpočtu.

• Pravidlo č. 1: V grafickém znázornění a matematickém vyjádření je foton reprezentován radiusvektorem (Feynman ve své knize ho přirovnává ručičce stopek).
• Pravidlo č. 2: Délka radiusvektoru fotonu je úměrná druhé odmocnině pravděpodobnosti jevu, v kterém foton vystupuje. Jinými slovy radiusvektor je také délky, že plocha čtverce nad ním je úměrná pravděpodobnosti jeho příspěvku ke konečnému výsledku (Obr.2).
• Pravidlo č. 3: Pravděpodobnost výskytu fotonu v daném místě D detektoru je dána vektorovým součtem jeho radiusvektorů po všech možných trasách, přičemž tato pravděpodobnost je úměrná kvadrátu délky součtového vektoru (Obr.2). Samozřejmě foton absolvuje jen jednu trasu, která víc než jistě není ani jedna z cest zahrnutých do výpočtu.
• Pravidlo č. 4: Fáze radiusvektoru (úhel φ) fotonu má stejnou hodnotu při vstupu na každou možnou trasu ze zdroje světla, jelikož se jedná o jeden a ten samý foton. Podél trasy se fáze radiusvektoru mění úměrně kmitočtu světla a "optické" délce trajektorie od zdroje světla k detektoru. Optická délka je L = L₀ c₀/c, kde L₀ je geometrická délka, c₀ je rychlost fotonu ve vakuu a c v látkovém prostředí. Více je o optické délce řečeno v stati Lom paprsků světla, a zejména v oddílu Rozptýlené trasy fotonu, kde se komentuje také pojem rychlosti světla c v látkovém prostředí.
  
• Pravidlo č. 5: Pro každý foton ve svazku platí samostatně Pravidlo č. 4. Svazek fotonu jen zesiluje účinky světla (jas), neovlivňuje např. tvar interferenčních obrazců nebo proporce jasu bodů v obraze zrcadla. Proto také skupině fotonů přisuzujeme jeden radiusvektor. Podle tohoto pravidla každý foton ve svazku je "autonomní", neovlivněný druhým fotonem, a jejich radiusvektory se nesčítají. Sčítání radiusvektorů jednotlivých fotonů znamená předpokládat, že detektor si "počká", až všechny fotony dorazí na místo, aby vyhodnotil jejich účinky. O tomto pohledu pojednává oddíl Interference - diskuse.
  
• Pravidlo č. 6: Trasu fotonu (svazku fotonů) kreslíme ve tvaru přímky, pokud podmínky pokusu nevyžadují změnu. Přímočará trajektorie (paprsek světla) je fiktivní trasa fotonu, která se zavádí z pragmatických důvodů a úzce souvisí s pojmem rychlosti světla - viz oddíl Rozptýlené trasy fotonu.

Půvab Feynmanovy metody analýzy účinků světla spočívá v její názornosti a nenáročnosti na matematický aparát. Žádné parciální diferenciální rovnice a operátory. V zde prezentovaných programech vystačíme jen se znalostí vlastností pravoúhlého trojúhelníka, jmenovitě funkcí sinus a Pythagorovy věty. Namísto integrálu se používá jen součet vektorů, což Feynmanovy slovy znamená zaháknutí začátku jedné šipky ke konci jiné. Pro vektorový součet platí komutativní zákon, což znamená, že vektor součtu nezávisí na pořadí připojování vektorů. Zato však sumarizační křivka (Cornuova spirála) získává roztodivný tvar v závislosti na sledu výpočtu a připojování jednotlivých vektorů. Tvar sumarizační křivky nemá žádný fyzikální význam a vypovídá jen o postupu výpočtu.