Lom paprsků světla

Člověku stojícímu po kolena ve vodě se jeho nohy zdají kratší. Vlnová teorie světla to vysvětluje postulátem, podle kterého světlo v látkovém prostředí se šíří přímočaře, avšak se sníženou rychlostí c oproti rychlosti c₀ ve vakuu. Toto zmenšení rychlosti se kvantifikuje empirickou látkovou konstantou zvanou index lomu: n = c₀ / c. Pro vzduch je n = 1,00029, pro vodu kolem 1,33, pro sklo cca 1,5. Velký index lomu vykazuje diamant: n = 2,417. Větší pozornost souvislosti rychlosti světla v látkovém prostředí a přímočarosti světelných paprsků jsme věnovali v oddílu Rozptýlené trasy fotonu.

Podle kvantové elektrodynamiky je foton nejmenší částice světla, která letí rychlostí světla c₀. Zdánlivé snížení rychlosti v látkovém prostředí je vyvoláno tím, že foton se v tomto prostředí pohybuje po klikaté trase, a tak mu to trvá déle, než by mu to trvalo při letu po přímce, jak to ilustruje Obr. 3. Kdybychom se nechtěli spoléhat na závěry oddílu Rozptýlené trasy fotonu, museli bychom počítat s rozptylem fotonu elektrony, obdobně jak to ukážeme v oddílu Rozptyl fotonu elektrony, ve sklíčku.

Program lom-paprsku.exe modeluje lom paprsků světla z pohledu QED (Obr. 9). Podobně jako vlnová teorie i zde je trasa fotonu (svazku fotonů) znázorněna přímkovými paprsky, avšak pro výpočet fáze radiusvektorů je délka trasy v látkovém prostředí L = L₀ c₀ / c, kde L₀ je fiktivní přímková trasa. Od rozhraní pokračuje foton po přímce k detektoru vzduchem (prakticky vakuem). Doba letu fotonu od zdroje k detektoru je součet doby letu v látce a ve vzduchu. Podobně je úhel otočení radiusvektorů složen ze součtu jeho fáze v látce a ve vzduchu.

Na Obr. 9 jsou zobrazeny trasy, říká se jim optické trasy, od zdroje k detektoru. V spodní části je znázorněn diagram doby letu fotonu od zdroje světla k detektoru po jednotlivých možných optických trasách. Zde jsou taky znázorněny radiusvektory fotonu (svazku fotonů) po dopadu na detektor. Jejich součet je zobrazen vpravo nahoře. Netradičně je zdroj světla umístěn v látce (ve skle nebo vodě), jelikož zde každý objekt může být zdrojem světla odrazeného od vnějšího osvětlení. Jen s velkou fantazii bychom si mohli představit, že v látce je zabudován nějaký detektor, i když oko člověka je možný detektor i ve vodě.

K délce součtového radiusvektoru nejvíc přispívají radiusvektory optických tras v okolí nejkratší doby letu fotonu. Představíme-li si v roli detektoru oko člověka, pak ten se dívá na zdroj ne po přímce ke zdroji, ale po nejkratší optické trase, čím vzniká u něho dojem, že zdroj světla je blíže k rozhraní dvou látek (vzduch-voda).

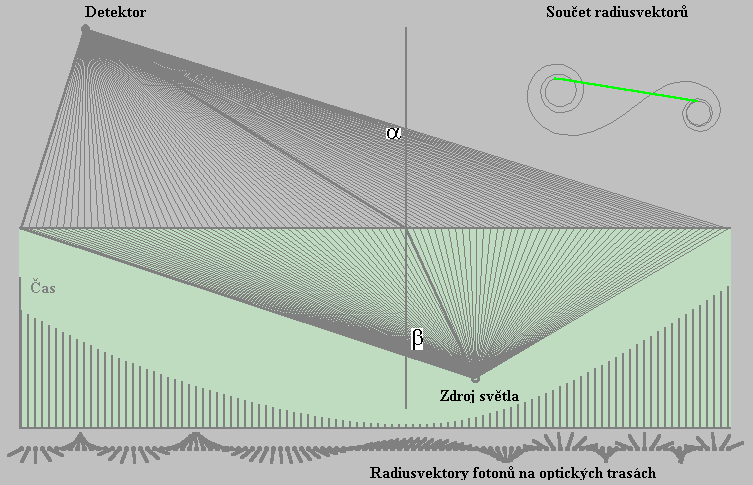
Obr. 9  Lom paprsků světla - program lom-paprsku.exe.

Časově nejkratší optická dráha na Obr. 9 ilustruje také Snellův zákon lomu geometrické optiky n = c₀/c = sinα/sinβ, podle kterého, laicky řečeno: "paprsek se láme ke kolmici v prostředí s větším indexem lomu".